안 쓰던 블로그
자료구조-힙heap 본문
HEAP
완전 이진 트리에 있는 노드 중에서 특정 노드(키 값이 가장 큰 노드나 가장 작은 노드)를 찾기 위해서 만든 자료구조
최대 힙 max heap
키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리 (이진 트리: https://foxtrotin.tistory.com/184 )
{부모 노드의 키 값>자식 노드의 키 값}
루트 노드: 키 값이 가장 큰 노드
최소 힙 min heap
키 값이 가장 작은 노드를 찾기 위한 완전 이진 트리
{부모 노드의 키 값<자식 노드의 키 값}
루트 노드: 키 값이 가장 작은 노드
힙과 이진 트리와의 관계

포화 이진 트리: 완전 이진 트리에서 모든 노드가 꽉 차 있는 트리
완전 이진 트리: 포화 이진 트리에서 노드 몇 개가 빠진 트리
힙: 포화 이진 트리일 수도 있고, 완전 이진 트리일 수도 있음
힙의 예

최대는 루트가 가장 큼, 최소는 루트가 가장 작음
힙이 아닌 이진 트리의 예

왼쪽 트리에서는 8의 오른쪽 자식인 4노드가 왼쪽 자식이 없기 때문에 완전 이진 트리가 되지 않아 힙도 아님
완전 이진 트리가 되려면 모든 노드가 차 있꺼나 맨 아래 1값 노드가 4의 왼족 자식 노드여야 가능
오른쪽 트리에서는 값이 제각각이라 힙이 아님
힙의 추상 자료형


최대 힙을 기준으로 추상 자료형을 보면
데이터는 '완전 이진 트리'와 '부모 노드의 키값>자식 노드의 키값'을 만족해야 한다
공백 힙을 생성
공백인지 검사
원소 삽입
원소 삭제 후 반환 하는 작업을 가진다
힙 구현
삽입 연산
1. 완전 이진 트리의 조건이 만족하도록 다음 자리를 확장 (추가할 자리에 노드 만듦)
노드가 n개인 완전 이진 트리에서 다음 노드의 확장 자리는 n+1번 노드다
n+1번 노드를 확장하고, 그 자리에서 삽입할 원소를 임시로 저장한다
2. 부모 노드와 크기 조건이 만족하도록 삽입 원소의 위치를 찾음 (자기 자리 찾아감)
현재 위치에서 부모 노드와 비교하며 크기 관계를 확인한다
{현재 부모 노드 키값 > 삽입 원소의 키값} 관계가 성립되지 않으면 서로 자리를 바꾸면서 제 자리를 찾는다
예를 들어 17을 삽입하는 경우
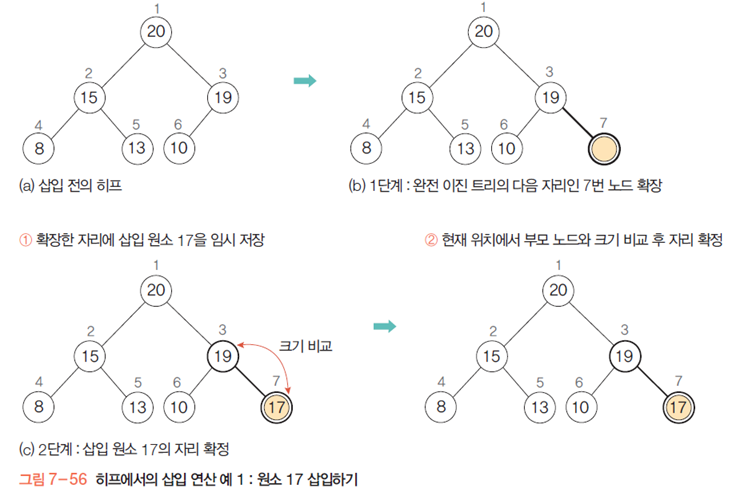
완전 이진 트리의 무게를 맞출 수 있는 곳인 오른쪽 맨 아래 노드에다가 17짜리 노드 추가
값 비교 하면서 17이 있어야 할 자리로 옮긴다. 여기서는 움직이지 않았다
27을 삽입하는 경우

23을 완전 이진 트리가 깨지지 않는 적당한 위치에 삽입한다
값을 비교하면서 자기 자리에 넣어준다
삽입 연산 알고리즘
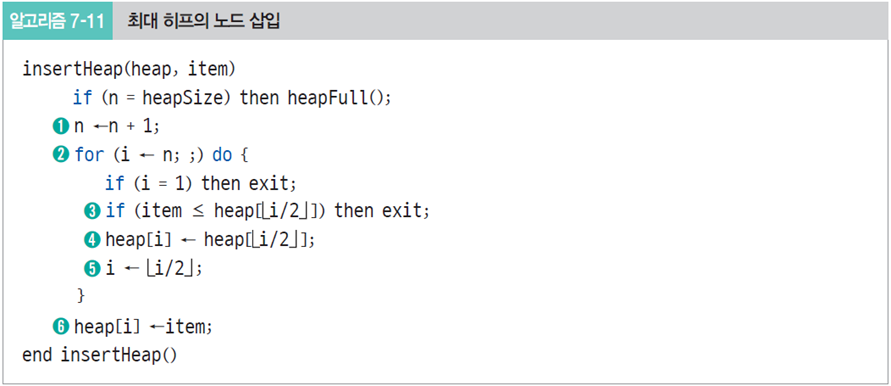
0. heap에다가 item을 넣을 건데, n==힙사이즈면 꽉 차있다는 의미(배열 구현이라 고정 크기)
1. 현재 힙의 크기를 하나 증가시켜서 노드 위치를 확장한다
2. 확장한 노드 번호가 임시 삽입 위치 i가 된다 for문을 돌면서
3. 삽입할 원소 item과 부모 노드 i/2의 값을 비교하면서 부모 노드보다 작거나 같으면 그대로(6번 단계로), 아니면 교환해야 한다(4번 단계로)
4. 삽입할 원소 item 부모 노드보다 큰 경우, 둘의 자리를 바꾼다. 먼저 값을 바꿀건데, 부모 노드의 값인 heap[i/2]를 현재 자리의 값인 heap[i]에다가 저장
5. 부모 노드 자리인 i/2를 i로 해서 다시 2~5번 과정을 반복하며 item을 삽입할 위치를 찾는다
6. 찾은 위치에 원소 item을 저장하고 삽입 연산을 종료한다
삭제 연산
힙에서는 루트 노드의 원소만을 삭제할 수 있다
1. 루트 노드의 원소를 삭제하여 반환
2. 원소의 개수가 n-1로 줄었으므로, 노드의 수가 n-1인 완전 이진 트리로 조정한다
-노드가 n개인 완전 이진 트리에서 노드 수 n-1개의 완전 이진 트리가 되기 위해서 마지막 노드인 n번 노드를 삭제한다
-삭제된 n번 노드의 원소는 비어있는 루트 노드에 임시로 저장한다
3. 완전 이진 트리 내에서 루트에 임시 저장된 원소의 제자리를 찾음
-현재 위치에서 자식 노드와 비교해서 크기 관계 확인
-{임시 저장 원소의 키값 > 현재 자식 노드의 키값}의 관계가 성립하지 않으면, 현재 자식 노드의 원소와 임시 저장 원소의 자리를 swap한다
삭제 예시


1. 루트 삭제
2. 마지막 노드 루트로 이동
3. 적당한 자리 찾아서 재배치
삭제 연산 알고리즘

0. heap의 노드를 지울 건데, 지울 노드가 없으면 error를 리턴
1. 루트 노드 heap[1]을 변수 item에 저장한다
2. 마지막 노드의 원소 heap[n]을 변수 temp에 임시로 저장한다
3. 마지막 노드 삭제로 배열 원소 개수(전체 힙 사이즈) -1
4. 마지막 노드의 원소였던 temp의 임시 저장 위치 i는 루트 노드의 자리인 1번으로. 탐색은 2번부터 할 것
5. 현재 저장 위치에서 왼쪽 자식 노드 heap[j]와 오른쪽 자식 노드 heap[j+1]이 있을 때, 둘 중 키 값이 큰 자식 노드와 temp를 비교해서 temp가 더 크거나 같으면 그대로(7번 과정으로), 아니면 교환할 것이다(6번 과정으로)
6. temp가 heap[j]나 heap[j+1]보다 작으면 자식 노드와 자리를 바꾸고 5~6번을 반복하며 temp의 자리를 찾는다
7. 찾은 위치에 temp를 저장하여 힙 재구성 작업 완료
8. 처음 삭제한 루트 노드를 저장한 변수 item을 반환하고 연산을 종료한다
힙의 구현
1차원 배열의 순차 자료구조를 이용하면 인덱스 관계를 이용하여 부모 노드를 찾을 수 있다(배열 같은 거)
순차 자료구조로 표현한 예
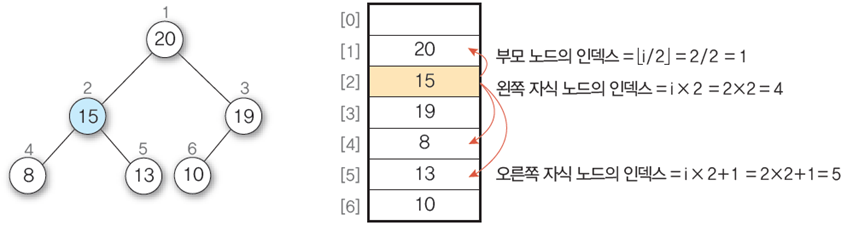
부모 노드의 인덱스 i/2
왼쪽 자식 노드 인덱스 i*2
오른쪽 자식 노드 인덱스 i*2+1
최종적으로 힙에 원소 다섯 개 10, 45, 19, 11, 96을 삽입하여 최대 힙을 구성하면 다음과 같다

1. 처음에 10 들어감
2. 45들어가면 2번 노드 자리에 삽입되는데, 10보다 크므로 10이 2번 자리로 45가 루트 노드가 된다
3. 19는 3번 노드 자리에 삽입되는데, 왼쪽 노드는 10이고 루트는 45니까 그대로 있는다
4. 11을 삽입하면 4번 자리에 들어간다. 11은 10보다 크니까 10과 자리를 바꾼다
5. 96을 삽입하면 5번 자리에 삽입이 된다. 11과 96을 비교하면 2번 자리가 96이 되고, 5번이 11이 된다. 96은 45보다도 크므로 1번 자리가 96이 되고 45가 2번으로 밀려난다
'알고리즘 > Algorithm' 카테고리의 다른 글
| 자료구조-그래프 순회(깊이 우선, 너비 우선) (0) | 2020.07.01 |
|---|---|
| 자료구조-그래프 (종류, 용어, 구현 방법) (0) | 2020.06.29 |
| [자료구조] 자가 균형 이진 탐색 트리: AVL트리 (나이 기준으로 사람 찾는 AVL트리 구현) (0) | 2020.06.19 |
| 자료구조-이진탐색트리 BST (0) | 2020.06.19 |
| 자료구조-트리 순회(전위 순회, 중위 순회, 후위 순회) (0) | 2020.06.16 |




