안 쓰던 블로그
[자료구조] 자가 균형 이진 탐색 트리: AVL트리 (나이 기준으로 사람 찾는 AVL트리 구현) 본문
트리 개념, 이진 트리, C로 트리 구현: https://foxtrotin.tistory.com/184
자료구조-트리 순회(전위 순회, 중위 순회, 후위 순회) https://foxtrotin.tistory.com/187
자료구조-이진탐색트리 BST https://foxtrotin.tistory.com/190
AVL트리가 왜 필요한가?
이진탐색트리 탐색의 특징 때문에 편향 트리에서 탐색 시간이 비효율적
예를 들어 저번 글의 코드에서 입력값이 이랬다

이런 경우 이쁘게 트리가 완성이 되어서 80을 찾는 데 50->70->80을 지나 3번만 탐색하면 된다
근데 아래 코드와 같은 입력일 경우
#include<stdio.h>
#include<stdlib.h>
typedef struct node {
int key;
struct node* left, * right;
} NODE;
int cnt = 0;
NODE* search(NODE* root, int key) {
cnt++;
if (root == NULL) return NULL;
if (root->key == key) return root; //key가 자기 자신인 경우 찾았으므로 리턴
else if (root->key < key) return search(root->right, key); //현재키<찾으려는 키면 오른쪽 트리로(큰수로)
else return search(root->left, key); //아니면 왼쪽 트리로
}
NODE* newNode(int item) {
NODE* temp = (NODE*)malloc(sizeof(NODE));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void inorder(NODE* root) { //중위 순회로 출력
if (root != NULL)
{
inorder(root->left);
printf("%d \n", root->key);
inorder(root->right);
}
}
NODE* insert(NODE* node, int key) {
if (node == NULL) return newNode(key); //트리가 비었다면 새로 노드를 만듦
if (key < node->key) node->left = insert(node->left, key); //찾는키<노드키면 왼쪽
else if (key > node->key) node->right = insert(node->right, key); //반대면 오르쪽
return node; //노드 포인터 반환
}
int main() {
NODE* root = NULL;
root = insert(root, 20);
insert(root, 30);
insert(root, 40);
insert(root, 50);
insert(root, 60);
insert(root, 70);
insert(root, 80);
cnt = 0;
search(root, 80);
printf("찾는 데 몇 번 순회?: %d\n", cnt);
inorder(root); //출력
return 0;
}
이 경우 만들어지는 트리의 형태는 다음과 같다


한 쪽으로 완전 치우친 편향 트리로 7번이나 탐색하게 된다
그래서 효율적인 탐색을 위해서는 트리가 항상 이쁘게 균형을 이룰 필요가 있다
AVL 트리의 개념
각 노드의 왼쪽 서브 트리의 높이hL와 오른쪽 서브 트리의 높이 hR의 차이가 1 이하인 트리
hL-hR 값인 높이 차이를 노드의 균형 인수(BF)라고 한다
균형 인수를 -1, 0, +1만 가지게 함으로써 균형을 항상 유지한다
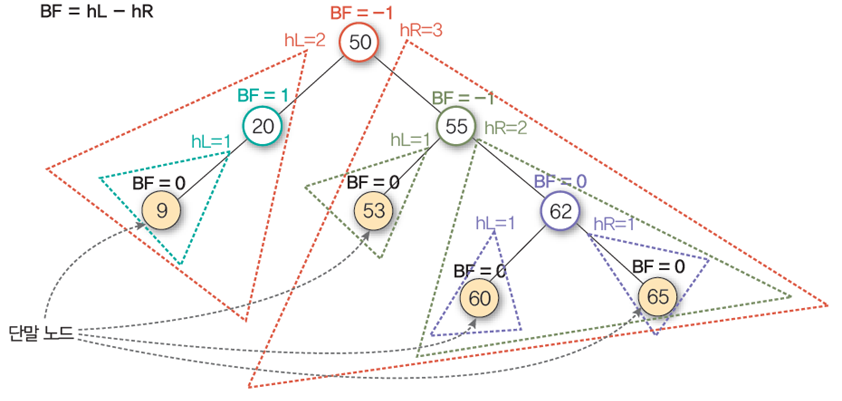
AVL 트리의 예

모든 노드가 균형 인수로 -1, 0, 1값을 가지므로 AVL트리다
균형이 깨져서 한 방향으로 치우쳤으므로 AVL트리가 아니다
균형 인수는 hL-hR로 구하니까 +값이면 왼쪽이 더 무거운 거고
-값이면 오른쪽이 더 무겁다는 의미가 된다
그러면 어떻게 균형을 맞추냐
높이가 맞지 않으면 돌려서 맞춘다
AVL 트리의 회전 연산
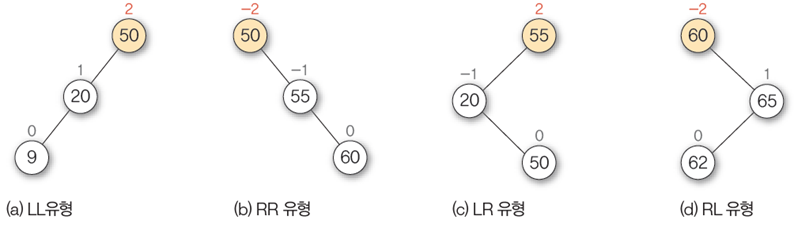
LL 회전 연산

왼쪽으로 편향되어 있을 때 쓰는 회전 연산
left-left라서 LL연산이라 부르고, 오른쪽으로 회전해야 한다
1. L2의 오른쪽 자식 노드를 L1의 왼쪽 자식 노드로 옮긴다 (NULL값을 옮기는 거 맞음)
2. L1을 L2의 오른쪽 자식 노드로 옮긴다
1번 과정이 끝나면 L2-L3 트리, L1 트리 이렇게 나눠짐
2번 과정에서 L1을 L2의 오른쪽에다가 붙임
NODE* rotate_LL(NODE* parent) { //LL회전(오른쪽으로 회전한다)
NODE* child = parent->left;
parent->left = child->right; //부모의 왼쪽 노드=자식 오른쪽 노드(부모에게는 NULL값이 왼/오에 달림)
child->right = parent; //부모를 자식의 오른쪽 노드로(자식 오른쪽에다가 부모 트리 연결)
return child;
}
RR 회전 연산

right-right로 자식이 붙어 있는 경우 왼쪽으로 돌려야 한다
LL연산과 완전 반대임
1. L2의 왼쪽 자식 노드를 L1의 오른쪽 자식 노드로 옮긴다
2. L1을 L2의 왼쪽 자식 노드로 옮긴다
NODE* rotate_RR(NODE* parent) { //RR회전(왼쪽으로 회전한다)
NODE* child = parent->right;
parent->right = child->left;
child->left = parent;
return child;
}
LR 회전 연산

자식 노드가 left-right 로 붙어 있는 경우 쓰는 회전 연산
1. L2와 L3 구간에 대해 RR연산
2. L3를 L1의 왼쪽 자식 노드로 붙이고 나면, LL연산을 쓰고 만드는 형태가 나옴
3. L1에 대해서 LL연산
NODE* rotate_LR(NODE* parent) { //LR회전(오른쪽-왼쪽으로 회전한다)
NODE* child = parent->left;
parent->left = rotate_RR(child); //자식 노드 RR회전해서 균형맞춤
return rotate_LL(parent); //부모를 LL회전해서 자식의 오른쪽으로
}2
RL 회전 연산

right-left 자식 노드
LR과 완전 반대
1. L2와 L3 구간에 대해 LL연산
2. L3를 L1의 왼쪽 자식 노드로 붙이고 나면, RR연산을 쓰고 만드는 형태가 나옴
3. L1에 대해서 RR연산
NODE* rotate_RL(NODE* parent) { //RL회전(왼쪽-오른쪽으로 회전한다)
NODE* child = parent->right;
parent->right = rotate_LL(child);
return rotate_RR(parent);
}노드의 높이를 구하는 연산
AVL트리는 균형이 깨졌을 때 회전 연산을 통해 균형을 맞춘다
균형이 깨졌다는 건 노드의 높이를 구해서 알 수 있다
노드를 기준으로 왼쪽 서브트리 높이와 오른쪽 서브트리 높이 차이가 2 이상일 때 균형이 깨졌다고 한다
int get_height(NODE* node) { //노드를 기준으로 트리의 높이 구하기
int height = 0;
if (node != NULL)
//NULL이 아니면 루트 1개는 무조건 있음
//max(왼쪽 높이, 오른쪽 높이)
height = 1 + max(get_height(node->left), get_height(node->right));
return height;
}노드를 기준으로 트리의 높이를 구했으니, 왼쪽과 오른쪽의 높이 차이를 구한다
int get_balance(NODE* node) { //균형이 되는 높이를 구함
if (node == NULL) return 0;
return get_height(node->left) - get_height(node->right); //왼쪽 서브트리 높이 - 오른쪽 서브트리 높이
}균형 맞추기
먼저 트리의 균형을 왼쪽-오른쪽 식으로 구한다
균형이 1보다 크면(왼쪽이 더 무거우면) 왼쪽 균형을 맞추고, 1보다 작으면(오른쪽이 더 무거우면) 오른쪽 균형을 맞춘다
-1~1사이라면 균형이 맞는 것이므로 그냥 반환한다
그리고 편향된 모습에 따라 LL/LR인지 RR/RL인지를 결정한다
마지막에 균형이 조정된 노드를 반환한다
NODE* balance_tree(NODE** node) { //트리의 균형 맞춤
int height = get_balance(*node); //왼쪽 높이-오른쪽 높이
if (height > 1) { //왼쪽이 더 크다면 왼쪽 서브트리 균형을 맞춤
if (get_balance((*node)->left) > 0) { //왼쪽 노드가 더 크면
//printf("LL\n");
*node = rotate_LL(*node); //오른쪽으로 돌림
}
else {
//printf("LR\n");
*node = rotate_LR(*node); //아니면 오른쪽-왼쪽으로
}
}
else if (height < -1) { //오른쪽 서브트리 균형을 맞춤
if (get_balance((*node)->right) < 0) { //오른쪽 노드가 더 크면
//printf("RR\n");
*node = rotate_RR(*node); //왼쪽으로 돌림
}
else {
//printf("RL\n");
*node = rotate_RL(*node); //아니면 왼쪽-오른쪽으로
}
}
//0이면 균형이 맞는 것이므로 패스
return *node;
}노드 검색
검색은 이진탐색트리의 검색과 같다
key값이 같으면 리턴, 작으면 왼쪽 크면 오른쪽
아래 코드에서는 찾기까지 탐색을 몇 번 했는지까지 cnt변수로 체크한다
int cnt = 0;
NODE* search(NODE* root, int key) {
if (root == NULL) return NULL;
cnt++;
printf("%d->", root->key);
if(root->key == key) return root; //key가 자기 자신인 경우 찾았으므로 리턴
else if (root->key < key) return search(root->right, key); //현재키<찾으려는 키면 오른쪽 트리로(큰수로)
else return search(root->left, key); //아니면 왼쪽 트리로
}노드 삽입
노드 구조체는 이렇게 구성되어 있다
typedef struct node {
int key; //나이
char sex; //이름, 성별(f,m)
char name[3];
struct node* left, * right;
}NODE;
insert함수의 매개변수로 데이터를 받는다
만약 노드가 없으면 노드를 먼저 만들어 준다
메모리를 할당하고 데이터 값을 넣고, 왼쪽 오른쪽 자식을 NULL값으로 초기화 한다
노드가 있다면 키 값을 비교한다
찾는 키 값이 더 작은 값이면 왼쪽 서브트리로, 크면 오른쪽 서브트리로 간다
여기서 BST와 AVL트리의 차이점이 나오는데,
AVL트리는 노드를 하나 넣고 균형을 맞추는 balance 함수를 호출한다
전체 코드
전체 코드는 아래와 같습니다
/*
20~100사이 난수 뽑음(나이)
들어온 난수 순서대로 나이를 기준(key)으로 성명, 성별을 갖는 이진탐색트리
이진탐색트리에서 특정 나이를 갖는 재난지원금 신청자 찾기
예) 20세 입력하면 20세 나이를 갖는 재난지원금 신청자의 정보 이진탐색트리에서 찾아서 보여줌
해당 신청자를 찾는데 몇 번 순회하는지 출력
*/
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
#include <list>
#include <algorithm>
using namespace std;
#define max(a,b) (((a)>(b)) ? (a):(b))
typedef struct node {
int key; //나이
char sex; //이름, 성별(f,m)
char name[3];
struct node* left, * right;
}NODE;
//AVL구현
NODE* rotate_LL(NODE* parent) { //LL회전(오른쪽으로 회전한다)
NODE* child = parent->left;
parent->left = child->right; //부모의 왼쪽 노드=자식 오른쪽 노드(부모에게는 NULL값이 왼/오에 달림)
child->right = parent; //부모를 자식의 오른쪽 노드로(자식 오른쪽에다가 부모 트리 연결)
return child;
}
NODE* rotate_RR(NODE* parent) { //RR회전(왼쪽으로 회전한다)
NODE* child = parent->right;
parent->right = child->left;
child->left = parent;
return child;
}
NODE* rotate_LR(NODE* parent) { //LR회전(오른쪽-왼쪽으로 회전한다)
NODE* child = parent->left;
parent->left = rotate_RR(child); //자식 노드 RR회전해서 균형맞춤
return rotate_LL(parent); //부모를 LL회전해서 자식의 오른쪽으로
}
NODE* rotate_RL(NODE* parent) { //RL회전(왼쪽-오른쪽으로 회전한다)
NODE* child = parent->right;
parent->right = rotate_LL(child);
return rotate_RR(parent);
}
int get_height(NODE* node) { //노드를 기준으로 트리의 높이 구하기
int height = 0;
if (node != NULL)
//NULL이 아니면 루트 1개는 무조건 있음
//max(왼쪽 높이, 오른쪽 높이)
height = 1 + max(get_height(node->left), get_height(node->right));
return height;
}
int get_balance(NODE* node) { //균형이 되는 높이를 구함
if (node == NULL) return 0;
return get_height(node->left) - get_height(node->right); //왼쪽 서브트리 높이 - 오른쪽 서브트리 높이
}
NODE* balance_tree(NODE** node) { //트리의 균형 맞춤
int height = get_balance(*node); //왼쪽 높이-오른쪽 높이
if (height > 1) { //왼쪽이 더 크다면 왼쪽 서브트리 균형을 맞춤
if (get_balance((*node)->left) > 0) { //왼쪽 노드가 더 크면
//printf("LL\n");
*node = rotate_LL(*node); //오른쪽으로 돌림
}
else {
//printf("LR\n");
*node = rotate_LR(*node); //아니면 오른쪽-왼쪽으로
}
}
else if (height < -1) { //오른쪽 서브트리 균형을 맞춤
if (get_balance((*node)->right) < 0) { //오른쪽 노드가 더 크면
//printf("RR\n");
*node = rotate_RR(*node); //왼쪽으로 돌림
}
else {
//printf("RL\n");
*node = rotate_RL(*node); //아니면 왼쪽-오른쪽으로
}
}
//0이면 균형이 맞는 것이므로 패스
return *node;
}
int cnt = 0;
NODE* search(NODE* root, int key) {
if (root == NULL) return NULL;
cnt++;
printf("%d->", root->key);
if(root->key == key) return root; //key가 자기 자신인 경우 찾았으므로 리턴
else if (root->key < key) return search(root->right, key); //현재키<찾으려는 키면 오른쪽 트리로(큰수로)
else return search(root->left, key); //아니면 왼쪽 트리로
}
NODE* insert(NODE** node, int key, char name[], char sex) {
if (*node == NULL) {
*node = (NODE*)malloc(sizeof(NODE));
(*node)->key = key;
for (int i = 0; i < 4; i++) (*node)->name[i] = name[i];
(*node)->sex = sex;
(*node)->left = (*node)->right = NULL;
}
else if (key < (*node)->key) {
(*node)->left = insert(&(*node)->left, key, name, sex); //찾는키<노드키면 왼쪽
(*node) = balance_tree(node); //균형 맞춤
}
else if (key > (*node)->key) {
(*node)->right = insert(&(*node)->right, key, name, sex); //반대면 오르쪽
(*node) = balance_tree(node); //균형 맞춤
}
else {
printf("중복된 데이터로 삽입 실패");
}
return *node; //노드 포인터 반환
}
void inorder(NODE* root) {
if (root != NULL) {
inorder(root->left);
printf("%d세 이름: ", root->key);
for (int i = 0; i < 3; i++) printf("%c", root->name[i]);
; if (root->sex == 'f') printf(", 여자\n");
else printf(", 남자\n");
inorder(root->right);
}
}
int main() {
srand((unsigned)time(NULL));
char rand_name[7][3]; //랜덤 이름 생성
for (int i = 0; i < 7; i++) {
int j;
for (j = 0; j < 3; j++) {
rand_name[i][j] = 'a' + rand() % 26;
}
rand_name[i][j] = 0;
}
NODE* root = NULL;
root = insert(&root, 50, rand_name[0], 'f');
insert(&root, 30, rand_name[1], 'm');
insert(&root, 20, rand_name[2], 'm');
insert(&root, 40, rand_name[3], 'f');
insert(&root, 70, rand_name[4], 'm');
insert(&root, 60, rand_name[5], 'f');
insert(&root, 80, rand_name[6], 'f');
printf("모든 사람 오름차순 출력\n");
inorder(root);
while (1) {
int findAge = 0;
printf("\n찾고 싶은 사람의 나이는?(종료는 0) ");
scanf("%d", &findAge);
if (findAge == 0) exit(1);
cnt = 0;
NODE* res = search(root, findAge);
if (res == NULL) printf("\n그런 나이의 사람은 없습니다");
else {
printf("\n%d세 이름: ", res->key);
for (int i = 0; i < 3; i++) printf("%c", root->name[i]);
if (res->sex == 'f') printf(", 여자\n");
else printf(", 남자\n");
printf("\n총 %d번만에 찾았습니다\n", cnt);
}
}
}

20~80까지 저렇게 편향되게 넣어도
80을 찾았을 때 7번 찾지 않고 3번만 찾음
AVL트리가 잘 구현되엇다
AVL구조는 똑같은데 main에서 이름/나이/성별 뽑을 때 완전 난수인 코드는 깃허브
https://github.com/proqk/Data_Structure_Study/blob/master/Tree/AVL_Tree.cpp
'알고리즘 > Algorithm' 카테고리의 다른 글
| 자료구조-그래프 (종류, 용어, 구현 방법) (0) | 2020.06.29 |
|---|---|
| 자료구조-힙heap (0) | 2020.06.28 |
| 자료구조-이진탐색트리 BST (0) | 2020.06.19 |
| 자료구조-트리 순회(전위 순회, 중위 순회, 후위 순회) (0) | 2020.06.16 |
| 자료구조-트리 (트리, 이진 트리, C로 구현) (0) | 2020.06.10 |




