안 쓰던 블로그
자료구조-트리 (트리, 이진 트리, C로 구현) 본문
트리
원소들 간에 1:n 관계를 가지는 비선형 자료구조
원소들 간에 계층 관계를 가지는 계층형 자료구조
상위 원소에서 하위 원소로 내려가면서 확장되는 트리 모양 구조
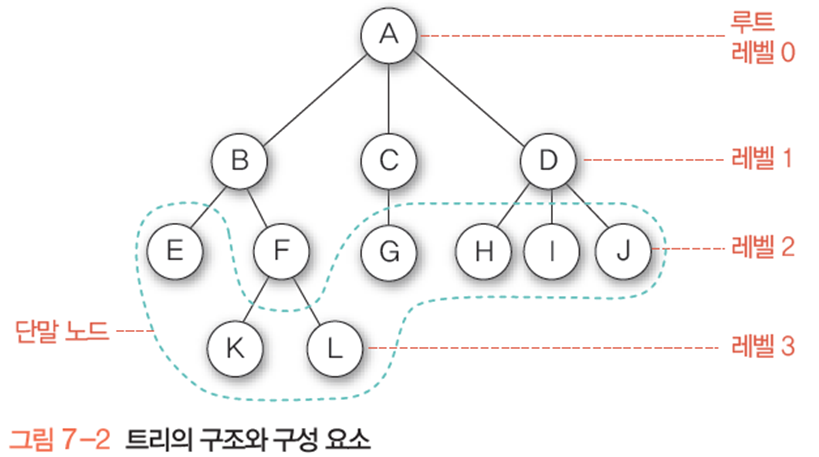
노드: 트리의 원소
-트리 A의 노드: A,B,C,D,E,F,G,H,I,J,K,L
루트 노드: 트리의 시작 노드, 레벨0
-트리 A의 루트 노드: A
간선: 노드를 연결하는 선, 부모-자식 노드 연결
형제 노드: 같은 부모 노드의 자식 노드들
-B,C,D는 형제 노드
조상 노드: 간선을 따라 루트 노드까지 경로에 있는 모든 노드들
-K의 조상 노드: F, B, A
서브 트리: 부모 노드와 연결된 간선을 끊었을 때 생성되는 트리
-각 노드는 자식 노드의 개수 만큼 서브 트리를 가짐
-D를 부모로 가지는 H,I,J는 D라는 서브 트리
자손 노드: 서브 트리에 있는 하위 레벨의 노드들
-B의 자손 노드: E,F,K,L
차수
-노드의 차수: 노드에 연결된 자식 노드의 수 (A의 차수는 3, B의 차수는 2, C=1, H, I, J=0)
-트리의 차수: 트리에 있는 노드의 차수 중에서 가장 큰 값 (트리 A의 차수는 3)
-단말 노드(리프 노드): 차수가 0인 노드. 자식 노드가 없다
높이
-노드의 높이: 루트에서 노드에 이르는 간선의 수=노드의 레벨 (B의 높이는 1, F의 높이는 2)
-트리의 높이: 트리에 있는 노드의 높이 중에서 가장 큰 값=최대 레벨 (트리 A의 높이는 3)
이진트리
트리의 모든 노드의 차수를 2 이하로 제한하여 전체 트리의 차수가 2 이하가 되도록 정의
이진 트리의 모든 노드는 왼쪽/오른족 자신 노드만 가짐
-부모 노드와 자식 노드 수와의 관계는 1:2
-공백 노드도 자식 노드로 취급
-0<=노드의 차수<=2

이진트리는 순환적 구성이다
=어느 서브 트리를 봐도 이진 트리다
노드의 왼쪽 자식 노드를 루트로 하는 왼쪽 서브트리도 이진 트리
노드의 오른쪽 자식 노드를 루트로 하는 오른쪽 서브트리도 이진 트리
일반 트리를 이진 트리로 변환 방법
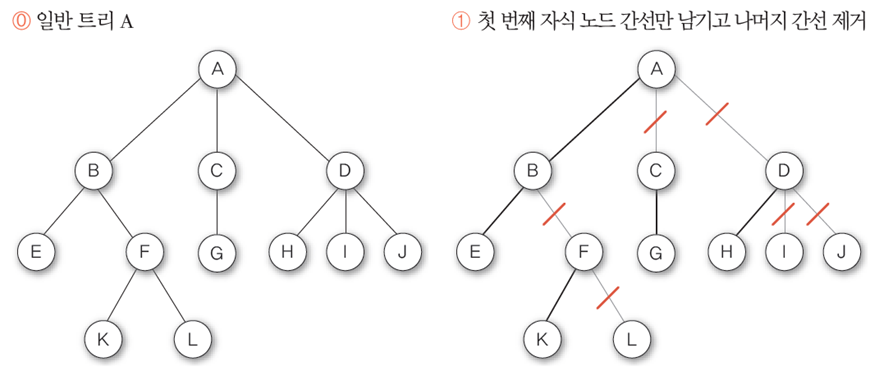
왼쪽 일반 트리 A의 차수는 3, D의 차수는 3
이진트리의 조건인 차수<=2 만족하지 않으므로 일반 트리
1. 첫 번째 자식 노드 B와 B의 첫 번째 자식 노드 E, F의 첫 번째 자식 노드 K.. 이런 식으로 남기고 나머지 전부 제거
C-G는 원래 하나 밖에 없어서 그대로
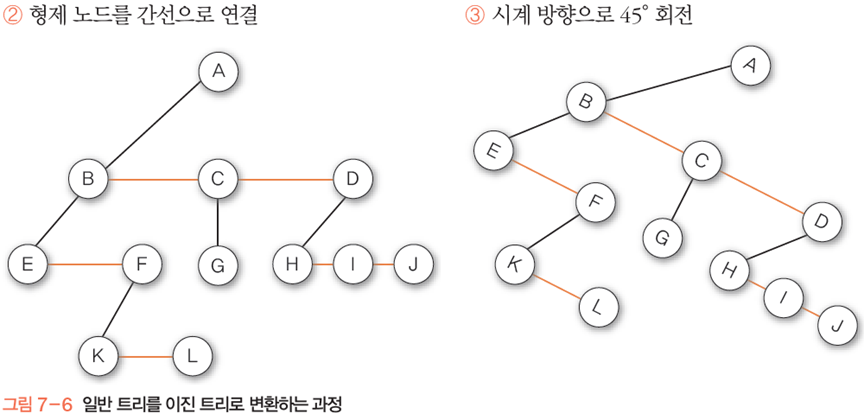
2. 형제 노드들끼리 연결한다
같은 부모에 있던 노드=형제 노드
3. 회전..은 그냥 트리 형태로 잡아준다는 의미
이진 트리의 특성
정의1) 노드가 n개인 이진 트리는 항상 간선이 n-1개
-루트를 제외한 n-1개의 노드가 부모 노드와 연결되는 한 개의 간선을 가짐
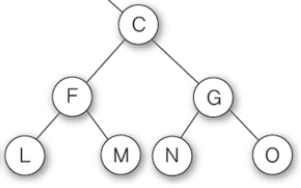
이런 트리가 있다면,
모든 노드에는 부모 노드로 올라가는 간선이 무조건 하나씩 있고, 루트만 없다
n개의 노드에서 루트 1개만 없으니까 n-1
정의2) 높이가 h인 이진 트리가 가질 수 있는 노드 개수는 최소 h+1개, 최대 2^(h+1)+1
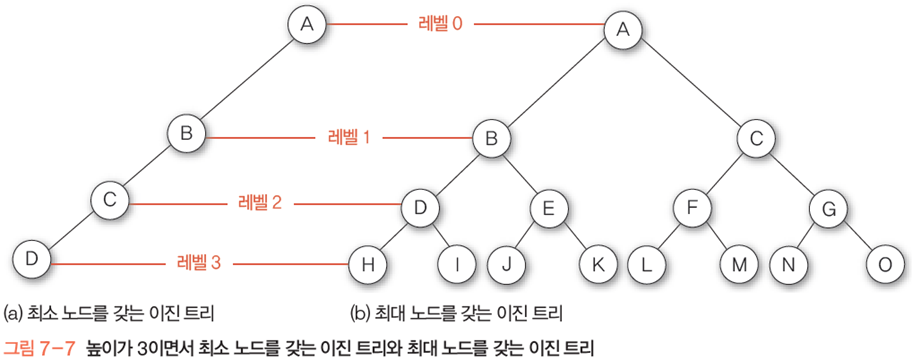
트리의 높이: 루트로부터 오는 간선의 개수. 그림에서는 간선이 3개니까 h=3
최소
-이진 트리의 높이가 h가 되려면 한 레벨에 최소 한 개의 노드가 있어야 함
-한 레벨 당 노드가 1개씩만 있다고 하면 노드가 최소가 되고, 이때 개수는 h+1
최대
-하나의 노드는 최대 2개의 자식 노드를 가질 수 있으므로 모든 노드가 자식을 2개씩 가지면 최대
-위에 그림에서 레벨0은 1개, 레벨1은 2개, 레벨3은 4개, 레벨4는 8개로
1, 2, 4, 8.. 즉 2^n형태로 늘어나므로 최대 노드의 개수는 레벨0부터 h까지 2^각 레벨한 값이 된다

그림에서 h=3이니까 2^0+2^1+2^2+2^3이고, 이진수로 1111이 된다
이진수 1111은 이진수 10000-1 과 같으니까(2^3 == 2^4-1)
일반화해서 2^(h+1)-1
이진 트리의 종류

포화 이진 트리
-높이가 h일 때 최대 노드 개수인 2^(h+1)-1의 노드를 가진 이진 트리
-모든 레벨에 노드가 포화상태로 차 있다
-루트를 1번으로 두고 2^(h+1)-1까지 정해진 위치에 대한 노드 번호를 가진다
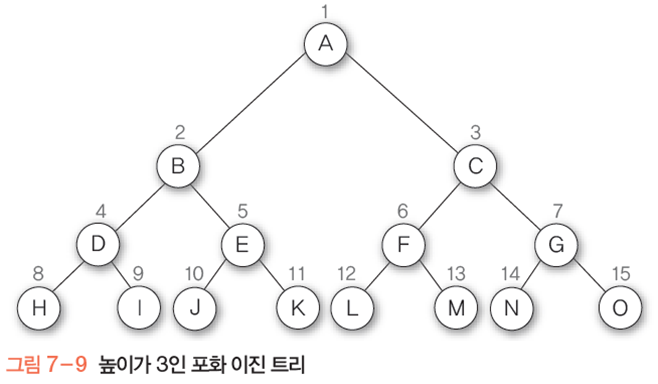
완전 이진 트리
-포화 이진 트리에서 노드 몇 개가 빠진 트리
-높이가 h고 노드 수가 n개일 때, 노드 위치가 포화 이진 트리에서의 노드 1번~n번까지의 위치가 완전히 일치하는 이진 트리
-n+1번부터 2^(h+1)-1번까지는 공백 노드다
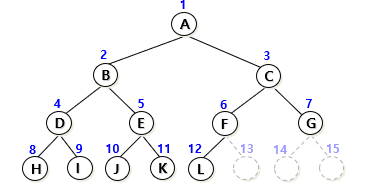
그림에서는 노드가 12까지밖에 없고, 1~12번 노드 번호는 위에 포화 이진 트리와 완전히 일치함
나머지 13, 14, 15는 공백 노드
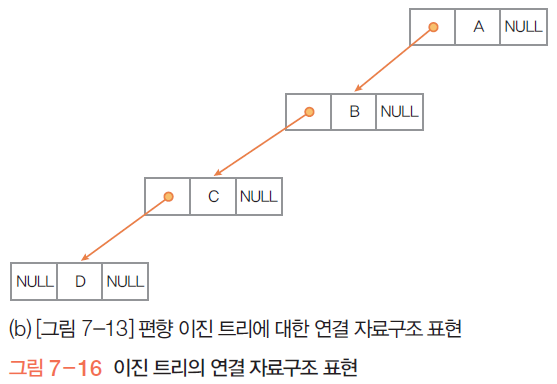
편향 이진 트리
-높이가 h일 때 최소 노드 개수인 h+1개 노드를 가지는 트리
-높이가 h일 때 h+1개의 노드를 가지면서 모든 노드가 왼쪽이나 오른쪽으로 쏠려 있다

참고로 트리가 이런 구조를 가지면 좋지 않다
이러면 차라리 링크드 리스트를 쓰는 게 좋다
순차 자료구조를 이용한 이진 트리의 구현
순차 자료구조: 배열, 링크드 리스트
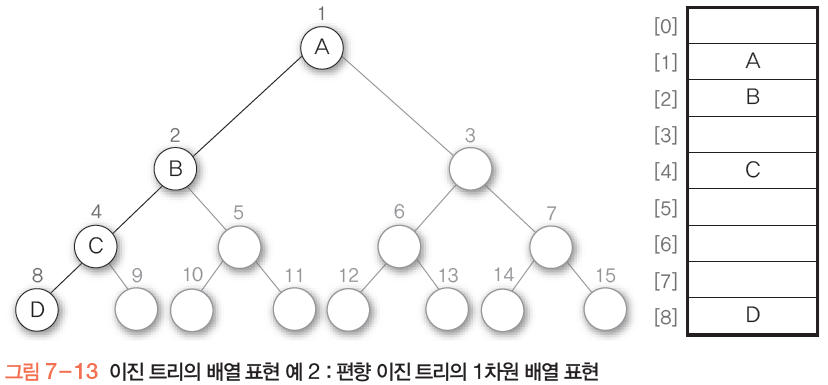
1차원 배열의 순차 자료구조 사용
높이가 h인 포화 이진 트리의 노드번호를 배열의 인덱스로 사용
인덱스 0번 : 실제로 사용하지 않고 비워둠
인덱스 1번 : 루트 저장

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | B | C | D | E | F | G | H | I | J | K | L |

만약 [5]=E에서 [2]=B로 가고 싶다면, E입장에서 부모 노드의 인덱스는 2
E에서 J로 가고 싶다면, E입장에서 왼쪽 자식 노드 J의 인덱스는 10
E에서 K로 가고 싶다면, E입장에서 오른쪽 자식 노드 K의 인덱스는 11
즉, i노드에서 부모로 올라갈 때: i/2하고 나머지 버림
i노드에서 왼쪽 자식으로 갈 때: i*2
i노드에서 오른쪽 자식으로 갈 때: i*2+1
성립 조건
노드 i의 부모 노드 성립 조건 i>1 : 루트 노드(1)보다 크면 갈 수 없다
노드 i의 왼쪽/오른쪽 자식노드 성립 조건 : 전체 노드의 개수 n보다는 작아야 한다
루트 노드 성립 조건 n>0 : 루트가 있다는 거는 노드는 최소 1개
이런 식으로 구현한다면 인덱스는
연결 자료 구조를 이용한 이진 트리 구현
포인터를 사용하여 이진 트리 구현
-데이터를 저장하는 데이터 필드+왼쪽 자식 노드를 연결하는 왼쪽 링크 필드+오른쪽 자식 노드 연결하는 오른쪽 링크 필드 구성
-자식 노드가 없으면 NULL 저장해서 NULL포인터로 설정

이런 식으로 완전 이진 트리를 만들면 아래와 같은 모습

편향 이진 트리를 만들면 아래와 같음
C로 실제 트리 구현
#include <stdio.h>
#include <stdlib.h>
typedef struct node //구조체 정의
{
int data;
struct node *left;
struct node *right;
}NODE;
/* newNode(): 노드에 메모리 할당하고 초기화*/
NODE* newNode(int data)
{
//노드에 메모리 할당
NODE* node = (NODE*)malloc(sizeof(NODE));
//데이터 넣음
node->data = data;
// 왼쪽, 오른쪽 노드를 NULL로 초기화
node->left = NULL;
node->right = NULL;
return(node);
}
int main()
{
/*루트 노드를 만든다*/
NODE *root = newNode(1);
/* 루트 노드를 만든 상태
1
/ \
NULL NULL
*/
root->left = newNode(2);
root->right = newNode(3);
/* 루트 노드1에 왼쪽, 오른쪽에 각각 2, 3이라는 자식 노드 추가한 상태
1
/ \
2 3
/ \ / \
NULL NULL NULL NULL
*/
root->left->left = newNode(4);
/* 2의 왼쪽 자식으로 4를 추가한 상태
1
/ \
2 3
/ \ / \
4 NULL NULL NULL
/ \
NULL NULL
*/
getchar();
return 0;
}https://github.com/proqk/Data_Structure_Study/blob/master/Tree/New_Tree.cpp
'알고리즘 > Algorithm' 카테고리의 다른 글
| 자료구조-이진탐색트리 BST (0) | 2020.06.19 |
|---|---|
| 자료구조-트리 순회(전위 순회, 중위 순회, 후위 순회) (0) | 2020.06.16 |
| 재밌는 C 포인터 문제 7개 (0) | 2020.06.03 |
| 알고리즘-스택 (C언어 배열로 구현한 스택, STL stack) (0) | 2020.05.30 |
| 알고리즘에서 쓰는 비트연산 (0) | 2020.05.22 |




