반응형
Notice
Recent Posts
Recent Comments
Link
안 쓰던 블로그
선형대수학-행렬식 determinant 본문
반응형
행렬에는 역행렬이 있는 행렬과 없는 행렬이 있다
역행렬이 있는지 어떻게 알 수 있나? 바로 행렬식을 통해 알 수 있다
1. 2x2 행렬에서 행렬식

A라는 2x2행렬이 있으면 A의 행렬식은 det(A)라고 한다
det(A)는 ad-bc 이고,
이 값이 0이면 역행렬이 없고 0이 아니면 역행렬이 있다
2. 3x3 이상의 행렬에서 행렬식-여인수 전개(cofactor expansion)
2x2행렬은 위와 같이 구하면 된다
3x3이상의 행렬에서는 여인수 전개라는 방법을 쓴다

A라는 3x3행렬이 있으면 이걸 2x2행렬 3개로 쪼갠다
어떤 기준으로 쪼개냐면 맨 윗 행을 수 하나를 기준으로 그 수랑 같은 행/열을 뺀 4개의 수가 2x2행렬 1개가 된다
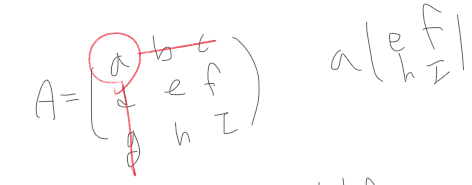
이렇게 하나

이렇게 하나

이렇게 하나 해서 3개
그리고 이 3개를 풀어서 +, -, +

예시

이러면 역행렬이 존재한다
문제 풀어보기

다음 3x3행렬과 이차방정식이 같음을 증명하시오

반응형
'수학' 카테고리의 다른 글
| 1~4차 행렬식 계산 방법, 행렬식 문제 풀이 몇 가지 (0) | 2020.10.19 |
|---|---|
| 3차 행렬식 더 쉽게 구하는 방법 (0) | 2020.10.19 |
| [선형대수학] 역행렬, 역행렬 변환, 존재유무-쌩초보 눈높이 설명 (0) | 2020.05.16 |
| [기초 수학 및 통계]-3. 역행렬과 선형변환 (0) | 2020.01.30 |
| [기초 수학 및 통계]-2. 행렬, 벡터의 연산 (0) | 2020.01.11 |
Comments




