안 쓰던 블로그
퍼셉트론, 신경망, 활성화 함수, 선형/비선형 기본 개념 정리 본문
기본 개념을 되짚어보며 정리
참고한 책: Deep Learning from Scratch
퍼셉트론
인공 뉴런, 단순 퍼셉트론이라고도 한다
다수의 신호를 입력으로 받아 하나의 신호를 출력한다 (인공지능을 말할 때 흔히 보았던 뉴런 이미지를 생각하면 된다)
여기서 말하는 신호는 흐른다/안 흐른다 두 가지 값을 가진다
입력 신호가 노드=뉴런에 보내질 때 각각 고유한 가중치가 곱해지고, 임계값=세타를 넘어설 때 1, 아니면 0이 된다

임계값을 반대로 넘기고 $b$로 기호를 치환하면 편향이 된다. 이 식을 $h(x)$라는 함수를 거치면 다음과 같이 표현할 수 있다
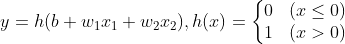
이 때, $h(x)$를 활성화 함수라고 한다
퍼셉트론으로 AND, NAND, OR을 구현할 수 있다
이 3가지 게이트를 그래프로 그려 보면, 직선 하나로 결과값의 영역을 나눌 수 있다
이런 직선의 영역을 선형 영역이라고 한다
그런데 XOR 게이트는 직선 하나로 결과값의 영역을 완벽하게 나눌 수 없다
이 경우에는 '직선'이라는 제약을 없애어, '곡선'을 사용하면 나눌 수 있다
이러한 곡선의 영역을 비선형 영역이라고 한다
다층 퍼셉트론
AND, NAND, OR 게이트를 단층 퍼셉트론이라고 한다
이 3가지 게이트를 조합하여 XOR 게이트를 구현할 수 있다
XOR 게이트는 0, 1, 2층으로 이루어져 있으므로 이는 다층 퍼셉트론이다
(XOR의 퍼셉트론은 총 3층으로 구성되지만 가중치를 갖는 층은 2개 뿐이라 2층 퍼셉트론이라 부른다. 문헌에 따라 3층 퍼셉트론이라고 하기도 한다)
신경망
퍼셉트론만 있어도 복잡한 함수를 표현할 수 있지만, 가중치 값을 적절히 정하는 작업은 여전히 사람이 몫이다
이런 가중치 매개변수의 적절한 값을 데이터로부터 자동으로 학습하게 한 것이 신경망이다
활성화 함수가 핵심 역할을 한다. 활성화 함수는 입력 신호의 총합이 활성화를 일으키는지를 정한다
1. 계산 함수
단순 퍼셉트론은 계산 함수를 활성화 함수로 채용한다
위에서 보았던, 입력이 0이 넘으면 1을 출력, 그 외에는 0을 출력하는 함수가 바로 계단 함수다
그래프를 그려보면 0을 경계로 출력아 0에서 1 또는 1에서 0으로 바뀐다
그 형태가 마치 계단같아서 계단 함수라고 명명되었다
2. 시그모이드 함수
다층 퍼셉트론인 신경망에서 자주 사용하는 함수는 시그모이드 함수다

$exp$는 자연상수 $e$를 의미하므로, 아래 식은 $1+e^{-x}$를 의미한다
그래프를 그려보면 0을 경계로, 입력이 작을 때는 출력이 0에 가깝고, 입력이 클 때는 출력이 1에 가깝다
이런 성질은 계단 함수와 동일하지만, 시그모이드 함수는 계단 함수와 '매끄러움'의 차이가 있다
입력에 따라 출력이 연속적으로 변화하여 부드러운 곡선의 형태를 갖춘다
sigmoid라는 이름은 S자 모양이라는 뜻이다
3. ReLU 함수
ReLU는 입력이 0을 넘으면 그 입력을 그대로 출력하고, 0 이하면 0을 출력하는 함수이다

R을 의미하는 Rectified 는 '정류된' 이라는 뜻이다
x가 0이하일 때를 차단하여 0을 출력한다는 의미에서 정류라는 단어를 사용한다
비선형 함수
계산 함수와 시그모이드, ReLU 함수는 전부 비선형 함수이다
즉, 직선 1개로는 그릴 수 없는 함수를 말한다
신경망에서는 활성화 함수로 비선형 함수를 사용해야 한다
선형 함수인 $h(x) = cx$를 활성화 함수로 사용한 3층 네트워크가 있다고 가정한다
이를 식으로 나타내면 다음과 같다

함수를 대입해 보면 다음과 같다
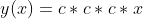
곱셈을 세 번 수행하지만, 실은 $y(x)=ax, a=c^{3}$와 같은 식이다
즉, 선형 함수를 여러 층으로 구성하여도 이점이 없다
그래서 활성화 함수로 비선형 함수를 사용하는 것이다
'머신러닝 > 머신러닝' 카테고리의 다른 글
| logistic regression back propagation derivative (로지스틱 회귀의 역전파 미분 유도 과정) (0) | 2021.08.21 |
|---|---|
| Transfer Learning과 함께 Image augmentation을 사용 가능할까? (0) | 2021.08.13 |
| 사전 훈련된 CNN 사용하기 (Using a pretrained CNN) (0) | 2021.07.16 |
| model.summary() 의 ValueError: This model has not yet been built 에러 (0) | 2021.07.16 |
| 다중 슬롯머신 문제 (Multi-Amred Bandits, MAB) with UCB1(Upper Confidence Bound1) (0) | 2021.06.24 |



