안 쓰던 블로그
백준 12995 트리나라 본문
트리나라는 n개의 도시로 이루어져 있고 각 도시 1~n은 모두 연결되어 있다
직원 k명이 전부 이사를 가야 하는데 모든 직원이 서로 다른 도시로 가야 해서 k개의 이사할 도시를 정해야 한다
k개의 도시는 모두 연결되어 있어야 한다
이사할 도시 k개를 고르는 방법의 수를 구하는 문제
k개 도시를 골라야 하면서 전부 연결되어 있어야 하니 다른 트리에서의 dp문제였던 트리의 독립집합이나 사회망 서비스와는 비슷하지만 다른 접근이 필요했다

예를 들어 k=15라고 하면 a, b서브트리에 13을 주고 c서브트리에 2를 줄 수도 있고
a에 2를 주고 b에 12를 주고 c에 1을 주는 방법도 있는 등 다양한 방법이 나올 수 있는데
이걸 어떻게 구현하느냐에 대한 문제였던 것 같다
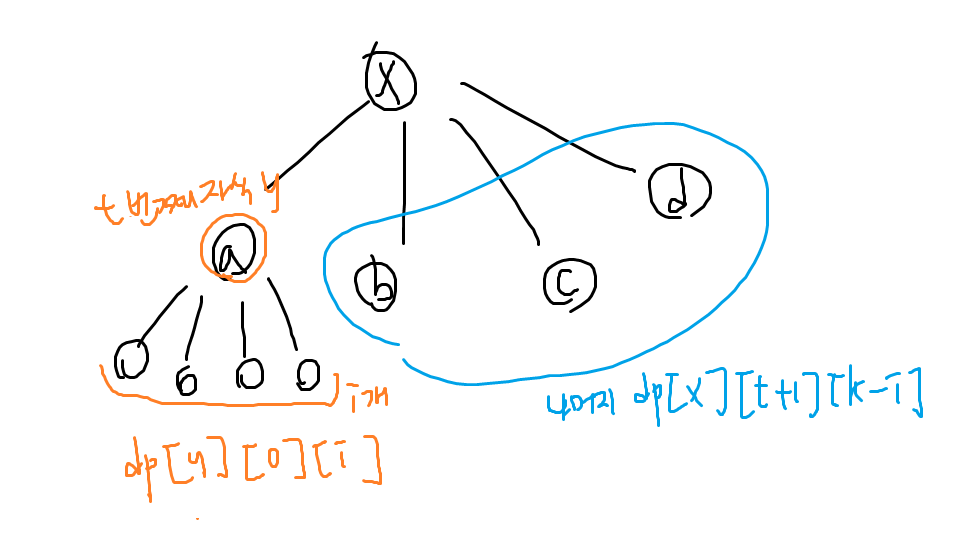
루트 x가 있을 때 자식을 무조건 첫 번째 서브트리와 나머지의 두 부분으로 나눠서 dp를 돌린다
자식 a,b,c가 있으면 처음에는 a와 b,c이고, 두 번째는 b와 c가 된다
이걸 체크하기 위해서 앞에서 몇 개의 서브트리를 처리 했는지에 대한 값 t를 추가해서 3차원 dp배열을 사용했다
$dp[x][t][k]=x$가 루트일 때, k개의 노드를 선택하는 방법의 수(처음 t개의 자식은 제외한다)
즉, t=0이라면 0개의 자식을 제외하니까 맨 처음 서브트리와 나머지로 나뉘게 되고
t=2라면 처음 2개의 자식을 제외하니까 세번째 서브트리와 나머지로 나뉘게 된다
t==x의 자식의 수 라면 더 이상 탐색할 서브트리가 없다는 의미로
x는 반드시 골라야 하니까 k=1일 때만 방법이 1개 있고 그 외의 경우에는 불가능하므로 0이다
하나의 서브트리와
t번째 서브트리를 $y$라고 한다면, y를 루트로 하는 서브트리에서도 0번째 자식부터 i개의 정점을 골라야 한다
$\sum dp[y][0][i]$
나머지
x를 루트로 하는 나머지 서브트리들에서도 t+1번째 자식부터 선택해야 하는 정점의 개수는 k-i개
$dp[x][t+1][k-i]$
최종 식은 다음과 같다
$dp[x][t][k]=\sum dp[y][0][i] * dp[x][t+1][k-i]$
전체 코드
#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
using namespace std;
int n, k;
long long dp[51][51][51];
bool chk[1000001];
vector<int> tmp[51], v[51];
void dfs(int now, int parent) { //부모-자식 관계 만들기
for (int next = 0; next < tmp[now].size(); next++) {
if (tmp[now][next] == parent) continue;
v[now].push_back(tmp[now][next]);
dfs(tmp[now][next], now);
}
}
long long dpdp(int x, int t, int k) {
long long& res = dp[x][t][k];
if (res != -1) return res; //이미 계산한 값은 패스
if (k == 0) return 1; //k개 도시를 다 골랐으면 끝
if (t == v[x].size()) { //더 이상 탐색할 도시가 없을 때
if (k == 1) return 1; //k가 1남았으면 루트 x를 고르는 경우 한 가지
else return 0; //그 외의 경우는 없다
}
res = 0;
for (int i = 0; i < k; i++) {
res += dpdp(v[x][t], 0, i) * dpdp(x, t + 1, k - i);
res %= 1000000007;
}
return res;
}
int main() {
ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
cin >> n >> k;
for (int i = 0, a, b; i < n - 1; i++) {
cin >> a >> b;
a--; b--; //0부터 시작
tmp[a].push_back(b);
tmp[b].push_back(a);
}
dfs(0, -1); //부모자식관계 트리를 만든다
memset(dp, -1, sizeof(dp));
long long ans = 0;
for (int i = 0; i < n; i++) { //모든 정점에 대해 계산한다
ans += dpdp(i, 0, k);
}
cout << ans % 1000000007;
return 0;
}'알고리즘 > 알고리즘 문제 풀이' 카테고리의 다른 글
| 백준 11282 한글, 11283 한글 2 (2) | 2020.10.16 |
|---|---|
| 백준 11284 초성 중성 종성, 11285 초성 중성 종성2 (2) | 2020.10.16 |
| 백준 2533 사회망 서비스(SNS)_dfs, dp (0) | 2020.10.02 |
| 백준 2213 트리의 독립집합 (0) | 2020.10.01 |
| 백준 14916 거스름돈을 푸는 다양한 방법 (2) | 2020.09.25 |


